利用示波器统计工具分析有噪声信号之平均和直方图-云帆兴烨

示波器通过测量产生的大量数据可做很多神奇的事情，可让你“识破”噪声并降低测量不确定度，对大量数据进行统计，奇妙的事情就会发生，虽然某些处理（如直方图）明显是基于统计学的，但某些统计工具是隐藏的，对任何一种情况，我们都可以利用示波器的统计分析功能。

方波上的噪声使得测量其幅度变得困难，幅度构成了其他测量的基础，例如宽度、上升时间、下降时间、过冲、甚至某种程度上频率和周期的测量。例如，上升时间测量信号从其幅度的10％变化到90％所需的时间，宽度是在信号幅度的50％处具有相反斜率的转变之间的时间差，因此，确定幅度对于几乎所有其他测量都至关重要。

如图所示，是对带有噪声的方波进行基本的示波器测量

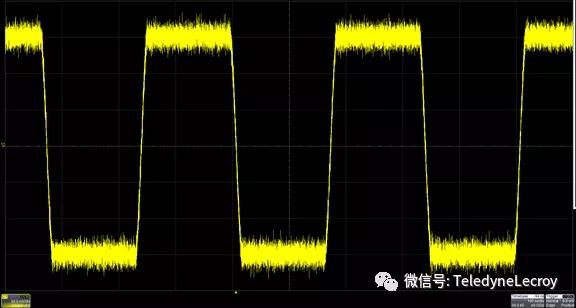
图方波上的噪声增加了测量信号幅度的难度

平均几乎所有示波器都提供平均功能，这是对波形最常见的统计处理方式，采集多个波形并逐点相加，然后将总和除以平均的波形数，得到波形的平均值，如图所示，最上面的波形是采集的原始波形，下方的波形是一千次采集的平均值，平均抑制了噪声，留下了干净的波形。

平均会将多个波形相加，并通过采集的波形数将总和归一化，从而降低了噪声对于高斯分布噪声，噪声幅度随着平均波形数量的平方根而减小，因此，一千个采集的波形将噪声幅度分量降低了31.6%或约30dB，平均过程的唯一缺点是需要采集大量波形。直方图

统计工具也可以量化不确定性。如果使用方波的每个样本值来创建其瞬时幅度值的直方图，我们就可以查看波形的结构，如图中的复合图形所示，生成直方图，旋转使其幅度比例垂直以匹配采集的波形，然后叠加在信号波形上。

生成直方图后，旋转直方图，使其与波形的顶部和底部幅值对齐，即使存在噪声，这样做也可以获得信号的幅度

直方图有两个峰值。一个对应于方波的最高电平，称为顶部，而另一个对应低电平或基值。各个直方图元素的平均值表示顶部和基值，方波的幅度是顶部和基值之间的差值，获得幅度后，可以计算所有其他脉冲参数，如图2所示。直方图统计工具可以让你透过数据的随机部分来从混沌噪声效应中提取有意义的信息，该技术适用于单次采集，不需要多次采集。当然，多次采集确实提高了测量的准确性。